Winnerless Competition in Clustered Neural Networks
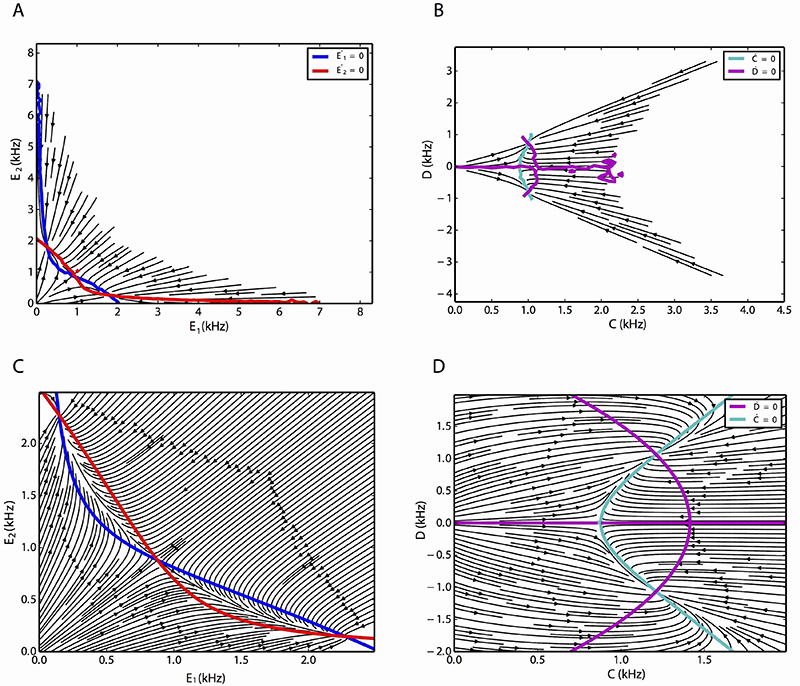
Flow of the two excitatory subnetworks in two dimensions, extracted from simulated time series (top) and inferred from the Lotka-Volterra model (bottom).
In her paper “Dynamics of competition between subnetworks of spiking neuronal networks in the balanced state”, Fereshteh Lagzi, PhD student at the Bernstein Center Freiburg, is taking a novel approach to the analysis of the dynamics between inhibitory and excitatory neuronal populations. Applying Lotka-Volterra equations, a mathematical model generally used in the analysis of predator-prey systems in animal populations, her paper creates a mathematical link between the non-linear dynamics of such ecosystems and the non-linear dynamics of populations of spiking neural networks.
Interdisciplinary and unconventional approaches are not uncommon at the Bernstein Center Freiburg. But Ferestheh Lagzi’s paper on the switching dynamics of neuronal networks can be considered one of the more innovative approaches in a variety of aspects. The biomedical engineer, who began her academic career at Polytechnic University in Tehran, joined the Bernstein Center Freiburg in 2010. Inspired by courses on artificial neural networks, which focused on the training of such systems in pattern recognition, solving complex problems in technical applications, Lagzi wanted to learn how biological brains accomplished such complex tasks: “I was interested in how population interaction can result in such interesting non-linear behaviors. Certainly, a linear system is not capable of performing these”, the neuroscientist explains.
Her determination to analyze the mathematics behind human cognition and behavior led Lagzi to take on a novel perspective on neural networks. Lagzi adopted Lotka-Volterra equations – a well-established mathematical model generally used for explaining population dynamics of species interactions in an ecosystem. “It is all a matter of perspective”, Lagzi explains. “In basal ganglia there are nuclei known to form populations of inhibitory neurons, whereas the cortex is usually modeled as a mixed excitatory-inhibitory population. The use of Lotka-Volterra equations enables us to explain nonlinear switching dynamics or oscillations between these subpopulations.” In this simplified model, the spikes generated by randomly connected populations of excitatory and inhibitory neurons take on the role of individuals in an animal population. “Excitatory neurons tend to increase, while inhibitory ones tend to decrease the probability of spike generation, and therefore population activity. This dynamics reflects, in essence, the relationship between prey and predator, which here specifically shows up as a winnerless competition.”
Balance between excitation and inhibition in healthy and diseased brains
The adaptation of Lotka-Volterra equations further enables Lagzi to incorporate a variety of different neuronal behaviors like oscillation or stationary activity. “We concluded that if such a model could account for spiking neural networks, this would provide a mathematically well-established foundation”, the researcher points out. Lagzi’s findings can be applied to the basal ganglia, but also a cortical column in the cortex, and thus contribute to the further understanding of cortical and subcortical networks. “Furthermore, it could be used as a model for understanding cognition, decision-making and other functions”, Lagzi adds. In the next step of her research, the final stage of her dissertation, the PhD student wants to improve this model. “Doing the analysis in three dimensions enables us to even better understand the collective behavior of the system. While our current two-dimensional model is able to explain switching dynamics, other interesting dynamics such as limit cycles, and chaotic behavior can only occur in a higher-dimensional system. This will make better predictions for networks composed of three, or more than three subnetworks.”
Furthermore, Lagzi sees the potential of her model in the treatment of diseases like Parkinson’s or epilepsy: “Here we are dealing with interacting populations where something goes wrong. We could say that the balance changes between excitation and inhibition, which affects the collective behavior of the system, is compromised. In Parkinson’s disease, for example, the collective behavior is oscillatory, where we would rather want to have stationary behavior. We want to understand under which conditions this oscillation emerges, and how we can restore normal conditions. Doctors would be able to improve their treatment through this knowledge.” Lagzi’s model can also explain phenomena like binocular rivalry, when each eye is exposed to a different stimulus and our perception of the stimulus alternates between the two possibilities.
Lagzi’s approach might finally yield back to the field of artificial neural networks. “Approaches inspired by spiking neuronal networks could lead to microchips based on this type of interaction at some point, because they consume less energy. Plasticity is another important aspect of this research because we are interested in teaching the network to do certain things and to adapt the way it learns and carries out its tasks. This might be a nice trajectory for future research.”
Original Publication
Lagzi F, Rotter S
“Dynamics of competition between subnetworks of spiking neuronal networks in the balanced state”
PLoS One 10 : e0138947
Figure Caption
Flow of the two excitatory subnetworks in two dimensions, extracted from simulated time series (top) and inferred from the Lotka-Volterra model (bottom).